Ondas

Existem vários tipos de ondas:

• Ondas sonoras: Propagação de oscilações locais da pressão e densidade de um meio material.

• Ondas eletromagnéticas: Propagação de oscilações do campo eletromagnético, propagam-se no vácuo.

• Ondas sísmicas: Propagação de vibrações das camadas da Terra.

• Fenómeno ondulatório: Propagação de energia através de um meio sem que haja transporte de massa.

Onda Periódica

1. A perturbação corresponde ao fenómeno ondulatório que se repete periodicamente no espaço e no tempo.

2. A frequência é caracteristica do emissor (não varia com o tempo), e é inversa do período.

$f = \frac{1}{T}$

3. Condição de propagação

$\phi(x, t) = \phi(x -vt)$

4. Condição de periodicidade

$\phi(x - vt) = \phi[(x + \lambda) -v(t + T)]$

5. Velocidade de fase

$v = \lambda f$

Propriedades das ondas

• Onda longitudinal: A grandeza física associada à onda varia no espaço segundo a direção de propagação. (Exemplo: som)

• Onda transversal: Grandeza fisica associada à onda varia no espaço segundo uma direção perpendicular à direção de propagação. (exemplo: onda eletromagnética) Estas ondas podem ser polarizadas segundo diferentes direções (no plano perpendicular à direção de propagação).

Equação de uma onda (de uma corda vibrante)

$\frac{\partial^2y}{\partial^2x^2} - \frac{1}{v^2}\frac{\partial^2y}{\partial t^2} = 0$

onde $v = \sqrt{ \frac{T}{\mu}}$ onde T é a tensão e $\mu$ é a massa por unidade de tempo.

Interferências

Interferência construtiva

$\phi_1(x,t) = Asin(kx-wt), \phi_2(x,t) = Asin(kx - wt + \alpha)$

Temos assim:

$\phi(x,t) = \phi_1(x,t) + \phi_2(x,t) = 2Acos\frac{\alpha}{2}sin(kx - wt + \frac{\alpha}{2})$

Interferência Destrutiva

$\phi_1(x,t) = Asin(kx - wt), \phi_2(x,t) = Asin(kx - wt + \pi) = - \phi_1(x,t)$

Logo $\phi(x,t) = \phi_1(x,t) + \phi_2(x,t) = 0$

Ondas estacionárias

$\phi_1(x,t) = Asin(kx-wt), \phi_2(x,t) = Asin(kx + wt)$

Temos:

$\phi(x,t) = \phi_1(x,t) + \phi_2(x,t) = 2Asin(kx)cos(wt)$

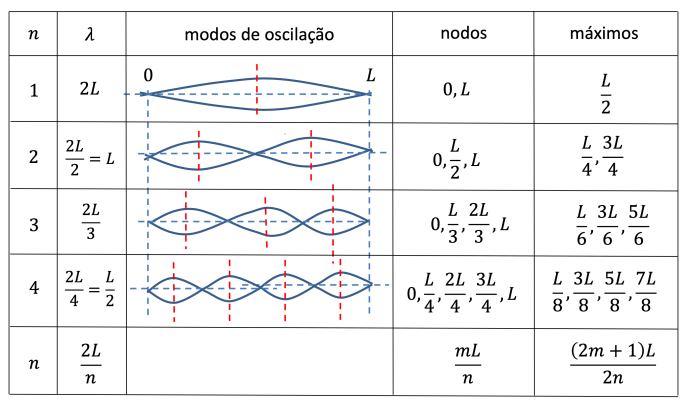
Fórmulas

$\text{Frequência Angular: w} = \frac{2\pi}{T}$

$\text{Nº de onda: k} = \frac{2\pi}{\lambda}$

$\text{Relação de dispersão: w} = k \times v$

$\text{Velocidade de grupo: Vg} = \frac{\partial w}{\partial K}$

Efeito Doppler

Definição

Alteração da frequência percecionada, ou medida, por um recetor devido ao movimento relativo entre esse recetor e uma fonte emissora.

• Afastamento entre fonte e recetor: Diminui a frequência.

$f' = f\frac{1}{1+{\frac{v_f}{v}}}$

• Aproximação entre fonte e recetor: Aumenta a frequência.

$f' = f\frac{1}{1-{\frac{v_f}{v}}}$

Reflexão e Refração

Reflexão: O ângulo de reflexão é igual ao de incidência.

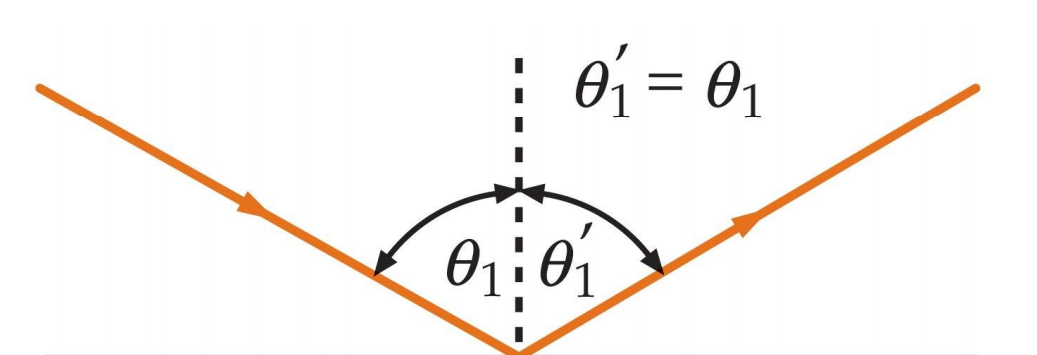
Refração: Desvio da direção de propagação da onda ao passar de um meio para o outro, em consequência da diferente velocidade de propagação nos dois meios. Quanto maior for essa diferença de velocidades, maior o desvio.

Fórmulas

$n_i seni = n_r senr$

$n = \frac{c}{v}$