Simetrias e Leis de Conservação

Princípio da Ação Mínima (Princípio de Hamilton)

O princípio de Hamilton diz nos que um sistema físico irá seguir, de entre todas as trajetórias possíveis, aquela que minimiza o integral S designado por Ação.

Lagrangiano

A função $\mathscr{L}$ designada função de Lagrange depende das coordenadas $r=(r_1,r_2,...,r_n)$ e respetivas derivadas $\dot r=(\dot r_1, \dot r_2,..., \dot r_n)$.

$\displaystyle \delta S = \delta (\int^{t_2}_{t_1} \mathscr{L}(r, \dot r, t)dt) = 0$

Em mecânica clássica, a função $\mathscr{L}$ é dada por:

$\displaystyle \mathscr{L}=T-U$

em que T e U representam, respetivamente, as energias cinética e potencial do sistema.

Demonstração das Leis de Newton

Usando o princípio da ação mínima e equações de Euler-Lagrange, é possível demonstrar todas as Leis de Newton

Voltando a Newton

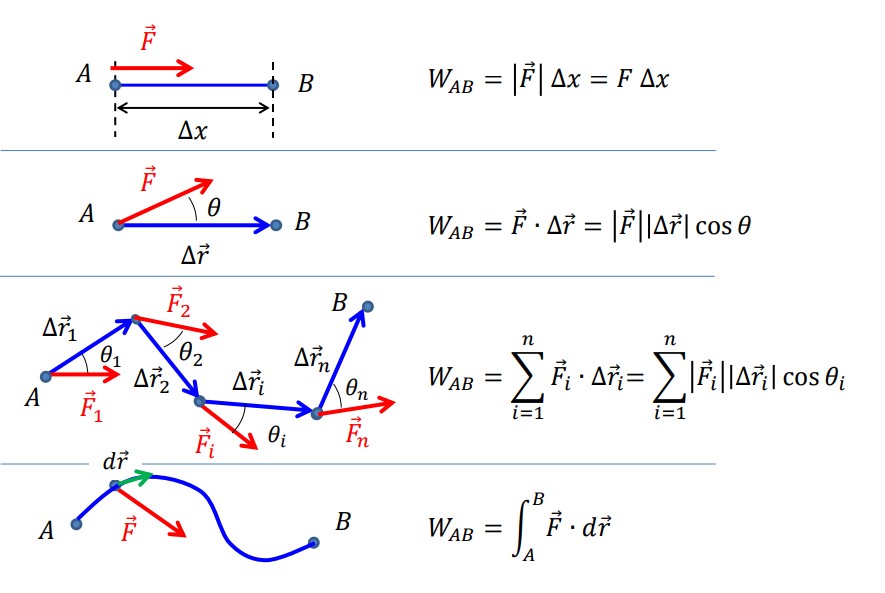
TIP

• O trabalho de uma força é igual à variação de energia cinética

$W_{AB}=\Delta E_c$

• O trabalho de uma força conservativa é igual à variação da energia portencial, pelo que não depende do caminho de aplicação da força.

Graus de liberdade e Coordenadas Generalizadas

Graus de Liberdade de um sistema correponde ao número mínimo de variáveis independentes necessárias para a descrição do sistema.

As equações de Euler-Lagrange podem ser escritas em função das variáveis generalizadas, $q_i$, correspondentes aos graus de liberdade do sistema.

$\frac{\partial L}{\partial q_i} - \frac{d}{dt}(\frac{\partial L}{\partial q_i}) = 0$

Por exemplo, no caso do pêndulo gravítico plano, as variáveis $x$ e $y$ não são independentes uma vez que a trajetória (circular) do pêndulo permite conhecer $x$ para um dado $y$ e vice-versa. Neste caso, utiliza-se apenas uma variável $(\theta)$ que define a posição do pêndulo. Diz-se então que o sistema tem apenas um grau de liberdade.

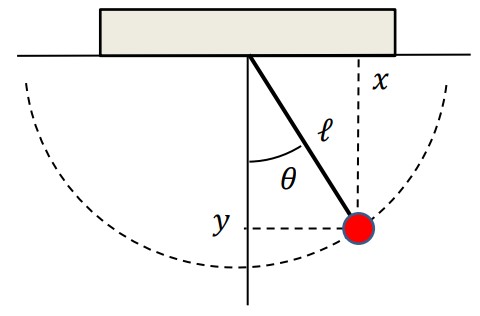
A partir desta imagem, de um pêndulo gravítico, podemos deduzir que:

$\begin{cases} x = l \sin \theta \\ y = l \cos \theta \end{cases} \implies \begin{cases} \dot x = l \ \dot \theta \cos \theta \\ \dot y = -l \ \dot \theta \sin \theta \end{cases}$

Forças de atrito

Como as forças de atrito têm sempre o sentido contrário ao da velocidade, o trabalho das forças de atrito é sempre negativo.

$\overrightarrow{F_\alpha} = -K_\alpha |\overrightarrow{v}^\alpha| \overrightarrow{e_v}$

• Atrito sólido - sólido: Quando $\alpha = 0$

$\overrightarrow{F_0} = - K_0 \overrightarrow{e_v}, K_0 = \mu |\overrightarrow{P}|$

• Atrito sólido - liquido (fluidos): Quando $\alpha = 1$

$\overrightarrow{F_\alpha} = - K_1 |\overrightarrow{v}| \overrightarrow{e_v}$

• Atrito sólido - fluido (alta velocidade): Quando $\alpha = 2$

$\overrightarrow{F_\alpha} = - K_2 |\overrightarrow{v}|^2 \overrightarrow{e_v}$

Revisões 12 ano - Fluidos (opens new window)

Energia Mecânica e Potência

A energia mecânica é dada pela soma da energia potencial com a energia cinética: $E = T + U$

Na ausência de forças exteriores $\frac {d}{dt} (T + U) = \frac {dE}{dt} = 0$ $\implies$ Lei da conservação da energia mecânica.

Assim, na presença de forças exteriores, a energia mecânica do sistema não se conserva:

$\frac {dE}{dt} = \sum F_i^{ext} r_i$

Se:

• A resultante das forças exteriores tem o mesmo sentido que o movimento, as forças exteriores fornecem energia ao sistema: $\frac {dE}{dt} > 0$

• A resultante das forças exteriores tem o sentido oposto ao do movimento, o sistema perda energia para o exterior (ex: Forças de atrito): $\frac {dE}{dt} < 0$

• A resultante das forças é perpendicular ao movimento, força normal no caso do pendulo. $\frac {dE}{dt} = 0$