Estabilidade e Movimentos Oscilatórios

Estabilidade de um Sistema

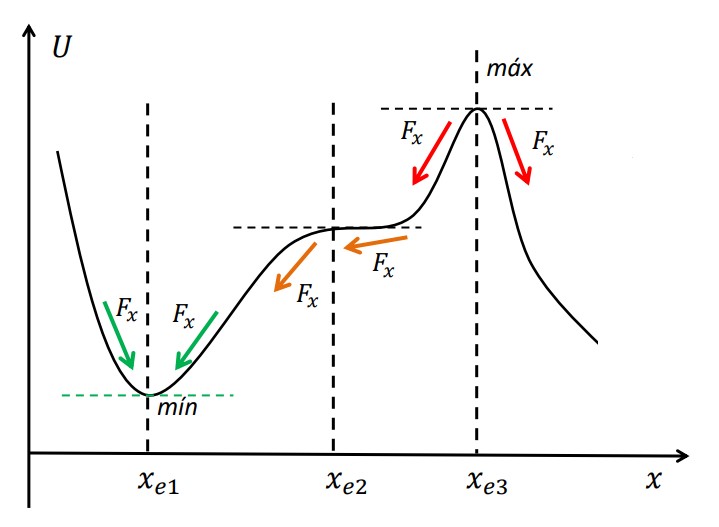
Mínimo - Equação Estável

Para $x_{e_1}$ tem-se que: $\begin{cases} F_x > 0 \text{ para } x < x_{e_1}\\ F_x < 0 \text{ para } x > x_{e_1} \end{cases}$

Nota:

Na vizinhança de um ponto de equilíbrio estável, a força tende a repor a condição de equilíbrio quando o sistema é afastado dessa condição.

Máximo - Equação Instável

Para $x_{e_3}$ tem-se que: $\begin{cases} F_x < 0 \text{ para } x < x_{e_1}\\ F_x > 0 \text{ para } x > x_{e_1} \end{cases}$

Ponto de Inflexão - Equação Instável

Para $x_{e_2}$ tem-se que: $\begin{cases} F_x < 0 \text{ para } x < x_{e_1}\\ F_x < 0 \text{ para } x > x_{e_1} \end{cases}$

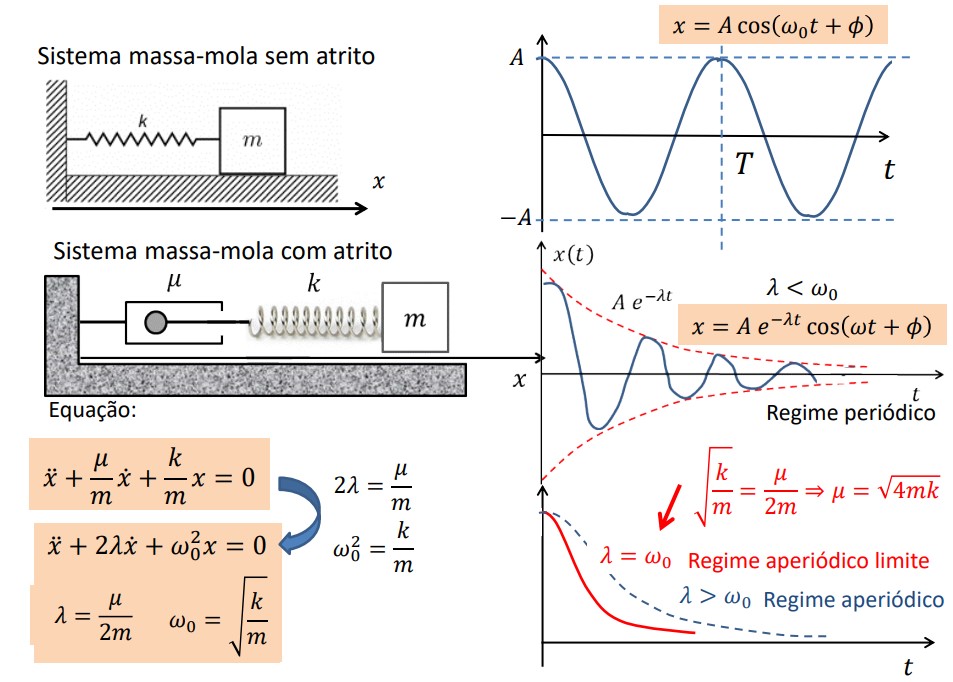
Oscilador Harmónico

Arbitrando $U_0 = 0$ e $x_e = 0$, temos que a Energia Potencial do Oscilador Harmónico é dada por:

$U(x) \appro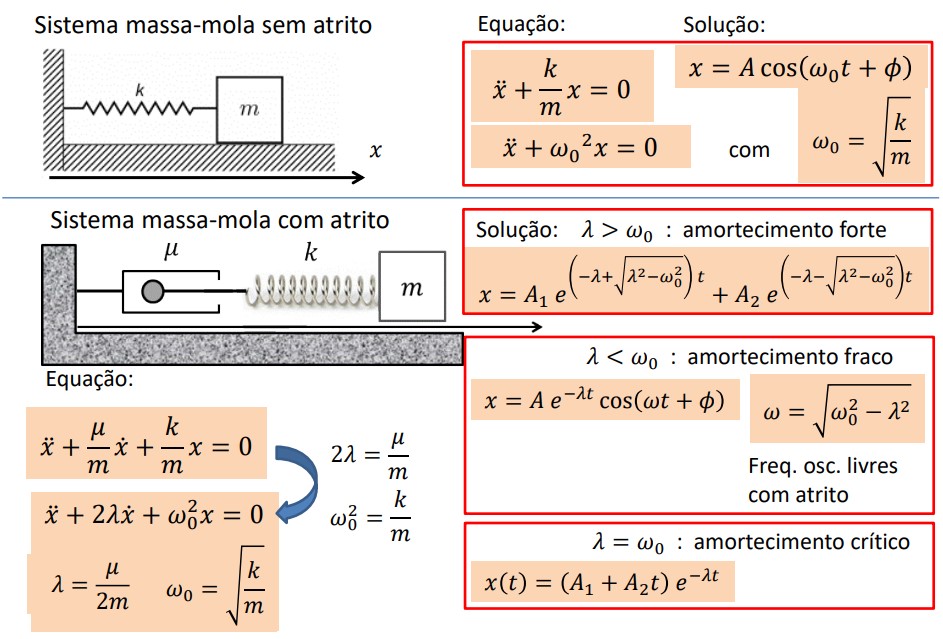xeq \frac{1}{2}kx^2$

Nota:

A Energia Mecânica total conserva-se no movimento harmónico simples (sem atrito)

Ou seja, E = T + U = constante $\implies \frac{1}{2}mv^2 + \frac{1}{2}kx^2 = \text{constante}$