Análise de projetos de investimento

Investimento: Aplicação atual de recursos, com o objetivo de obter benefícios futuros. Estes benefícios podem corresponder a:

• Fluxos financeiros: Dinheiro (cash-flows).

• Investimentos sociais: Estradas, educação, saúde.

• Aplicações em ativos financeiros (compra de ações) ou reais (ex: apartamentos).

Na análise de projetos procura-se avaliar genericamente uma afetação de recursos (R), feita inicialmente, é capaz de vir a gerar uma sucessão de benefícios líquidos (B) que excedem esse investimento inicial.

Concentrando num domínio puramente financeiro R e B representam dinheiro, fluxos financeiros negativos e positivos (CF- ou CF+). Sendo que CF são Cash Flows.

Idealmente, estaremos mais interessados em investir em projetos em que a soma dos CF- seja inferior à soma dos CF+. O problema é que esta análise é dependente do tempo e, com o tempo,o dinheiro está sujeito a determinados fatores como, por exemplo, a inflação e os juros. Para sabermos lidar com estes fatores, de modo a comparar CF em diferentes momentos precisamos de aprender alguns princípios do Cálculo Financeiro.

Cálculo financeiro

Juro: Renumeração cobrada pelo empréstimo de dinheiro (ou outro item), existem dois tipos de juro.

• Juros Simples: A taxa de juros é aplicada sobre o valor inicial de forma linear em todos os períodos, ou seja, não considera que o valor sobre o qual incidem juros muda ao longo do tempo.

$jC_0 + C_0 = (1 + j)C_0$

Em que j é a taxa de juro anual e o $C_0$ é o capital inicial-

• Juros Compostos: Juros corrigíveis de cada período são somados ao capital para o cálculo de juros nos períodos seguintes. Neste caso, o valor da dívida é sempre corrigido e a taxa de juros é sempre calculada sobre esse novo valor.

$C_n = C_0(1 + j)^n$

Em que n é o número de anos.

No caso destes juros pode ocorrer o processo de capitalização, que permite chegar de forma inversa à noção de atualização, em que se faz o cálculo do valor atual (VA) ou presente de dinheiro a receber no futuro, sendo a respetiva taxa designada por taxa de atualização.

$VA = \frac{C_n}{(1 + r)^n}$

Em que $C_n$ é o valor a receber daqui a x anos e r a taxa de juros.

Inflação e taxas reais

É preciso ter noção que a taxa de juro pode ir variando ao longo dos anos, não sendo necessariamente constante, um dos fatores que pode causar essa alteração é a inflação. As taxas de inflação podem incorporar a noção de inflação ou não.

• Taxa de juro nominal (jn): Usa-se em avaliação de projetos a preços correntes, não é corrigida tendo em conta o efeito da inflação.

• Taxa de juro real (jr): Taxa nominal expurgada do efeito da inflação.Usa-se em avaliação de projetos a preços constantes

$jr = \frac{1 + j_n}{1 + i} - 1 \approx j_n - i$

Taxas de juro nominais e efetivas

É também possivel trabalhar com períodos infra-anuais, usando na atualização uma taxa de juro equivalente, isto é, uma taxa efetiva que aplicada ao mesmo capital inicial conduz ao mesmo capital final.

$(1 + j_k)^k = 1 + j_a$

TAN: Eventuais pagamentos ou recebimentos infra-anuais são calculados de forma proporcional, mas não equivalente do ponto de vista financeiro.

Por exemplo:

Quando TAN = 12%

$J_m = \frac{12\%}{12} = 1$

A taxa mensal equivalente à taxa anual efetiva (TAE) é:

$j_m = (1 + j_a)^1/12$

TAEG: Taxa anual efetiva global, inclui encargos como seguros de vida e taxas adicionais associados ao empréstimo.

Equivalências das taxas de juro. Duas taxas de juro referidas a períodos diferentes de capitalização são equivalentes quando aplicadas ao mesmo capital, produzem o mesmo resultado no mesmo período de tempo. É dada por:

$(1 + j_k)^k = 1 + j_a$

Em que $j_k$ é a taxa do sub-periodo k e k é o número de subperíodos do periodo.

Anualidades e perpetuidades

Numa situação em que os valores dos cash-flows se repetem ao longo do tempo, estamos perante anuidades e perpetuidades que se distinguem pelo facto de a sequência de cash-flows ser limitada no tempo ou ser infinita, respetivamente.

Anuidade é uma designação que pode ser utilizada quer a frequência de cash-flows seja anual ou não. Numa situação em que se obtém um empréstimo num período e temos rendas ou pagamentos constantes (Anuidades), durante n períodos com uma taxa de atualização, o cálculo do valor atual (VA) de todos os cash-flows dá-se por:

$\sum \frac{A_t}{(1 + r)^t}, t = 1,...,n$

Trata-se de um progressão geométrica que pode ser descrita na forma:

$VA = A\frac{(1 + r)^n - 1}{(1 + r)^n \times r} = Af(r,n)$

Em que $f(r,n)$ é o fator de anuidade e $n$ é a perpetuidade.

Quando $n = \infty$ estamos perante o valor atual de uma perpetuidade:

$f(r, \infty) = A \times \frac{1}{r}$

Estes casos excluem os casos de rendas crescentes. Tendo em conta rendas crescentes a uma taxa g < r, temos a anuidade:

$VA = A \times (\frac{1}{r - g} - \frac{(1+g)^n}{(1 + r)^n \times (r -g)})$

E a perpetuidade:

$VA = A \times \frac{1}{r - g}$

Por exemplo:

A Teresa possui um aqueduto que gerará 2 milhões de euros de fluxos de tesouraria durante o ano de 2020. Os custos de operação do aqueduto são negligenciáveis e a sua durabilidade muito grande. Infelizmente, o preço da água transportada tem diminuído e prevêse que os fluxos de tesouraria diminuam 4% ao ano. A taxa de atualização é de 10%. Qual é o valor atual dos fluxos de tesouraria do aqueduto se se assumir que os fluxos de tesouraria durarão para sempre?

Usando a fórmula de cima:

$2000000(\frac{1}{0,1 + 0,04}) = 14285714,29€$

Análise de rentabilidade de projetos de investimento

Investimento: Sequência de fluxos financeiros (cash-flows) distribuidos por diversos periodos. O primeiro cash-flow normalmente é negativo:

• Despesas de investimento: Terrenos, edíficios, equipamentos licenças e patentes ou, até em fundo de maneio, como a constituição e reforço de stocks de matérias primas ou mercadorias.
• No final de vida do projeto: O valor destas despesas que seja recuperável dará origem ao valor residual do investimento.

Valor residual do investimento: Gerado pela venda de um imobilizado no final do tempo de vida do projeto.

$VR = \text{Valor do mercado n} - (\text{Valor do mercado n} - \text{Valor contabilistico}) \times \text{Taxa de imposto}$

O valor de mercado é o valor esperado de venda do ativo no ano n e o valor contabilístico é:

$\text{Valor contabilistico} = \text{Valor de compra} - \text{Amortizações acumuladas}$

Os cash-flows durante a fase de exploração (passada a fase inicial de investimento) serão habitualmente positivos se o projeto for lucrativo.

$\text{CF exploração} = RAJI \times (1 - \text{Taxa de imposto}) + \text{Amortizações e depreciações}$

Em que RAJI corresponde ao resultado antes de juros e impostos, ou seja, o mesmo que EBIT, resultados operacionais.

Por exemplo:

1. A empresa MGM investiu 100 mil € numa nova máquina para os próximos 4 anos;
2. Esta é depreciável em 5 anos, findos os quais pode ainda ser vendida por 10 mil € (valor de mercado no ano 5);
3. Sabe-se que as vendas anuais adicionais serão de 150 mil € durante todo o projeto;
4. Os custos operacionais anuais adicionais com pessoal, fornecimentos e serviços externos e matéria prima serão de 100 mil €, acrescidos dos custos com amortizações (depreciações), 20%;
5. A taxa de imposto a pagar pela empresa é de 25%.

$VR = VM -(VM - VC)t = 10 - (10 - 20) \times 0,25 = 12,5$

$VC = \frac{100}{5}$

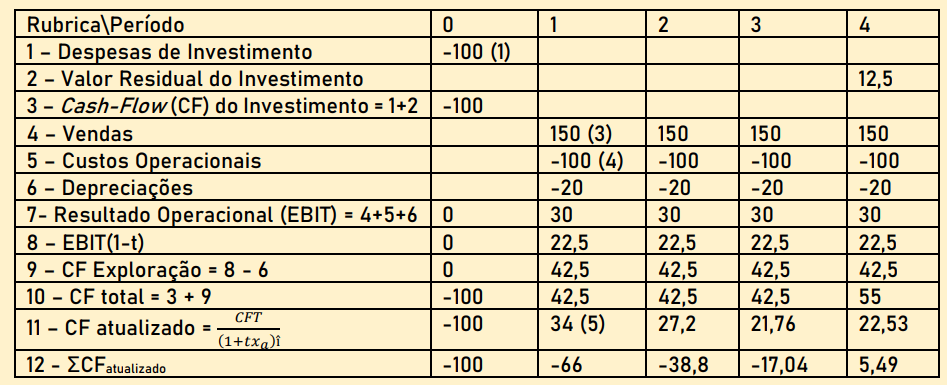
Quando o $RAJI < 0$:

• Projeto/ empresa não lucrativa o imposto não existe $t = 0$

• Projeto implementado por uma empresa lucrativa tem-se em conta o imposto e o cash-flow será negativo.

Na avaliação de projetos de investimentos estamos confrontados com a necessidade de comparar fluxos financeiros aplicados numa fase inicial, com fluxos gerados nos anos seguintes. Para isso usamos os seguintes indicadores:

1. Taxa de atualização: Exprime o custo de oportunidade do capital, ou seja, o rendimento que o investidor pretende tendo em conta o risco do investimento. São em geral nominais, aplicados a cash-flows a preços correntes. Quando os cash-flows são reais ou a preços constantes, utilizam-se taxas de atualização reais. A determinação das taxas de atualização devem ter em conta o risco associado ao investimento.

A taxa de atualização de um projeto financiado exclusivamente por capital próprio deve corresponder à soma de:

• Rendimentos esperados de ativos sem risco;
• Um prémio de risco inerente à atividade económica em causa e o risco financeiro associado ao grau de endividamento da empresa.

Quando houver financiamento com capital alheio:

• A taxa de atualização deve incorporar a taxa de juro da divida líquida de impostos.
• A taxa de atualização deve ser igual ao custo médio ponderado do capital, sendo a ponderação dada pelas percentagens dos dois tipos de capital, calculados ao valor de mercado.

Custo médio ponderado do capital ( CMPC ou WACC)

$\text{Taxa de atualização com financiamento misto} = r_CP \times CP\% + r_D \times (1 -t) \times D\%$

$r_CP$ é igual ao custo do capital próprio.

$CP\%$ é a percentagem de capital próprio.

$r_D$ é o custo de capital alheio líquido de um imposto.

$D\%$ é a percentagem de capital alheio.

$CMPC = \frac{C_\text{alheio}}{CP + C_{alheio}} \times r_D \times (1 - t) + \frac{CP}{CP + C_{alheio}} \times r_CP$

$r_D$ é o custo médio da dívida.

$t$ é igual à taxa de imposto.

$r_CP$ é a renumeração requerida pelos acionistas.

Por exemplo:

A empresa MGM tem um Capital Social composto por 10 000 ações, com um valor nominal 1 € cada. O valor do capital próprio em balanço é de 70 000 € e cada ação está cotada em 10 €. O financiamento com recurso a terceiros é constituído por um empréstimo bancário no valor de 50 000 € e 5 000 obrigações com um valor nominal de 1 € e cotação de 0.8.

1. Qual o valor de capital próprio relevante para cálculo do CMPC (Custo Médio Ponderado do Capital)?

O que importa não é o valor contabilístico (70 000 €), nem o valor do capital social realizado $10 000 \times 1 = 10 000 €$, mas o valor de mercado pelo qual seria possível comprar a empresa $10 000 \times 10 = 100 000 €$.

2. Qual o valor da dívida relevante para cálculo do CMPC (Custo Médio Ponderado do Capital)?

O que importa não é o valor contabilístico (do balanço), que seria de 55 000 € $50000 + 5 000 \times 1 €$, mas sim o valor de mercado que é igual a 54 000 € $50 000 + 0.8 \times 5 000€$.

3. Qual o valor das percentagens de capital próprio e alheio para cálculo do CMPC (Custo Médio Ponderado do Capital)?

$V= CP + D = 100000 € + 54000 € = 154000€$

$CP\% = \frac{CP}{V} = \frac{100000€}{154000€} = 65\%$

$D\% = 100 - 65 = 35\%$

4. Se a taxa de impostos sobre lucros for de 25%, o custo médio da dívida (rD) for de 5% e a remuneração requerida pelos acionistas (rCP) for igual à dos títulos do Estado de curto prazo (1.5%) + o prémio de risco de 6.5%, qual será o CMPC?

$CMPC = r_CP \times CP$

2. Valor Atual Liquido (VAL): Soma de todos os CF do projeto devidamente atualizados.

$VAL(r) = \sum \frac{CF_K}{(1 + r)^K}$

Em que CF = cash-flow e r a taxa de atualização

Se VAL(r) > 0, o projeto é rentável à taxa de atualização. Entre dois projetos A e B, se $VAL_A > VAL_B \to P_A \space \text {melhor que o} P_B$

Por exemplo:

O João comprou 100 ações da empresa MGM, tendo pagado 7€ por ação na expectativa de receber dividendos de $1€ \times 100$ nos anos 1 e 2, e de vender os títulos no ano 3 por 10€ cada. Sabendo que ações de empresas com idêntico grau de risco oferecem uma rentabilidade anual de 5%, calcule o VAL e diga se aconselha o investimento.

$VAL(5\%) = -\frac{700}{(1 + 0,05)^0} + \frac{100}{(1 + 0,05)^1} + \frac{100}{(1 + 0,05)^2} + \frac{1000}{(1 + 0,05)^3} = 349,78€$

O VAL é positivo, o investimento é rentável.

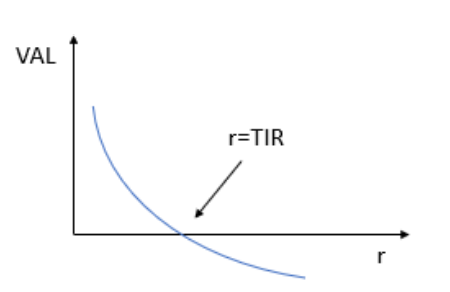
3. Taxa interna de rentabilidade (TIR): É a taxa r de atualização para a qual o VAL = 0, o seu cálculo resulta de um processo iterativo. Aceitar um projeto com $VAL(r) > 0$ significa aceitá-lo quando $TIR > R$.

Problemas no cálculo e utilização da TIR:

• Pode existir mais do que uma TIR. É o caso, por exemplo, da existência de cash-flows negativos intermédios ou finais (investimentos não convencionais).
• Não existir TIR.
• A TIR é inadequada para projetos mutuamente exclusivos, isto é, em que só podemos fazer um deles.

4. Periodo de recuperação do investimento (PRI): Tempo necessário para que os cash-flows atualizados gerados pelo projeto igualem o capital investido inicialmente.

$\sum = \frac{CF_K}{(1 + r)^K} = 0$

$PB = \text{Ano anterior a mudança de sinal no CFacumulado} - \frac{\text{útimo CFacumulado negativo}}{\text{CFatualizado no primeiro positivo}}$

5. Indice de rentabilidade

$IR = \frac{VAL + \text{Inventário Inicial}}{Inventário Inicial} = \frac{VA}{\text{Inventário Inicial}}$

Um projeto considera-se aceitável quando $IR > 1$. Tal como a TIR, este indicador peca na análise de projetos mutuamente exclusivos.